link

                               Origine de la gamme naturelle.

Nicolas Minet (Irem de Poitiers)

Do, ré, mi, fa, sol, la, si... On dit aujourd'hui de ces 7 notes qu'elles forment la "gamme diatonique de do majeur". Il serait faux de croire que le mysticisme du nombre 7 peut seul expliquer le choix . La tradition accorde à la "gamme de Pythagore" une place récurrente dans des textes de la Grèce Antique, relayés au Moyen Age par des personnages tel Boèce (VIème s.) ; cette gamme, ancêtre de nos gammes "diatoniques" aurait été élaborée à l'Ecole Pythagoricienne dans le cadre d'un culte voué aux nombres entiers et à la faculté qu'on leur prêtait de permettre la compréhension de l’Univers. L'objet de cette feuille à problèmes est de faire connaissance avec elle.
Toujours dans la Grèce Antique, des systèmes finalement proches de la gamme de Pythagore ont été proposés par des théoriciens tel Aristoxène (IIème s. av.J.C.), par une "division du canon" ; ce canon tout à fait pacifique est un instrument rudimentaire également appelé monocorde : le son est produit par une simple corde tendue au dessus d'une caisse de résonance en bois. On peut essayer en prenant une corde plus courte d'obtenir des sons consonants avec le son de départ ; des choix (arbitraires ? cf [1]) de systèmes de base à 4 notes, appelés tétracordes, ont été fait, et l’assemblage de deux tétracordes ayant une note commune a fourni des gammes à ... 7 notes !
Des nuances entre les gammes sont apparues (genres, modes,...), qui ont été conservées peu ou prou jusqu'au XVème siècle, quand des exigences liées à la transposition d'une mélodie sont devenues prioritaires. Pour autant, des gammes heptatoniques ont subsisté, même si d'autres nombres que 7 ont été utilisés : les pianistes nous étonnent sur un clavier organisé selon un schéma répétitif de 7 notes sur les touches blanches, touches blanches elles-mêmes interrompues par 5 touches noires selon une périodicité visible à l’œil nu.

Qu'on chante ou qu'on joue d'un instrument, on dispose d'un nombre variable de notes : si les pianistes n'ont pas d'autre issue que de jouer les 80 à 90 notes de leur clavier, c'est une infinité de notes qu’offrent la voix, un trombone, un violon... car si l’étendue des sons potentiels est limitée par la note "la plus grave" qu'on puisse produire et "la plus aiguë", aucune autre contrainte ne subsiste entre ces deux bornes. 
Parfois, on parle de "8 notes" en disant : do, ré, mi, fa, sol, la, si, do. Peut-on considérer que les deux "do" sont deux notes différentes alors qu'elles portent le même nom ? Bien sûr, le 2ème do est plus aigu que le 1er ; plus précisément, sa fréquence est double de celle du premier ; par exemple, on obtient l'un en pinçant une corde d'une longueur donnée, et l'autre en pinçant la même corde, mais deux fois plus courte. On dit que le 2ème do est l'octave du 1er , ou encore que l'intervalle entre des deux notes est une octave. 
Voici une première écoute : 
Un "Do" de référence, puis du "Do" à l'octave inférieure de 1er et enfin du "Do" à l'octave supérieure du 1er

On a ainsi une impression particulière de "ressemblance" en entendant ces notes. On s'autorise donc à leur donner le même nom, de sorte que notre honneur est sauf, comme on peut se contenter de raisonner "modulo 7 (notes)" , nous restons dans le thème de la feuille à problèmes : "autour du nombre 7 " !

Voici maintenant quelques expériences sonores afin de rencontrer la gamme de Pythagore :

Puisqu’il faut choisir des notes pour chanter ou jouer de la musique, repartons de celles que nous avons déjà entendues, à savoir des notes à l’octave l’une de l’autre ; prenons une corde dont nous notons 1 la longueur (l’unité). Nous produisons une note à l’octave (supérieure) de ce son si la corde est de longueur moitié. Petite parenthèse, il n’est pas très difficile de se fabriquer un monocorde : une caisse de résonance en bois, des trépieds pour ne pas la poser à même le sol, vis et mécanique de guitare (trouvables dans un magasin de musique) pour tendre la corde.

En l’occurrence, c’est plutôt un bicorde, avec deux cordes aux caractéristiques identiques : même diamètre, même longueur et même tension, produisant ainsi le même son. L’intérêt d’avoir deux cordes est de pouvoir faire une comparaison entre le son de référence, produit par la corde de longueur 1, et un autre son, obtenu en réduisant la longueur de la corde vibrante (sans la couper !) en utilisant un chevalet mobile :

Détail du monocorde (à droite, le chevalet mobile)

Nous dirons qu’une gamme se définit par une échelle de sons entre deux notes à l’octave l’une de l’autre, ce qui revient donc, en pensant "longueur de cordes", à choisir un ensemble de nombres compris entre 1/2 et 1 ...

note à  l'octave                                               note de départ

L’infini des possibilités peut laisser perplexe. Il faut donc se donner des critères de choix.
- Nous savons que 7 est un nombre de notes qui a été retenu par l’Histoire...
Que peut-on suggérer pour choisir " 6 nombres intermédiaires ?

La gamme de Pythagore

- Pythagore aurait choisi de prendre, après la moitié, le tiers de la corde ; mais 1/3 n'est pas compris entre 1/2 et 1, ce qui impose de prendre plutôt la note à l’octave inférieure, qui nous donne, on le sait, une impression similaire, d'où le choix du nombre 2/3 . Pour les Pythagoriciens, que des fractions avec les premiers nombres entiers 1/2 et 2/3 donnent des sons consonants avec le son émis par la corde de référence était un signe fort pour les retenir, car ce sont des lois numériques qui étaient censées permettre de comprendre l’Univers.

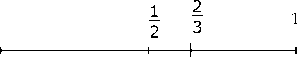
Deux notes, ce n'est pas assez pour faire de la musique... Pythagore aurait utilisé le principe suivant : puisque la corde de longueur 2/3 "sonne bien" avec la corde de départ, une corde de longueur " les 2/3 des 2/3 " donnera la même impression avec la corde de longueur 2/3... On obtient ainsi une corde de longueur 4/9. 
Mais comme 4/9 n'est pas compris entre 12 et 1, on prend le même son.. à l'octave inférieure en multipliant par 2 la longueur. On obtient donc une corde de longueur 8/9 :

Et ainsi de suite.......A vous de continuer (jusqu’où ?...)

Voici les rapports de la gamme de Pythagore (notation "américaine" des notes : C = do, D = ré, etc...)

Voici un instrument correspondant : chaque corde a pour longueur l’une des fractions ci-dessus.

Cette gamme de Pythagore a des avantages : elle utilise un principe naturel, celui de la voix humaine, dit des " quintes justes " ; traduction : la fraction 2/3, base de la construction de la gamme, est la cinquième note de la liste, une fois réordonnée (le sol (G) dans le schéma ci-dessus) ; c’est pourquoi ce cheminement est appelé le " cycle des quintes ". On peut signaler que ce cycle ne se referme pas car on ne retombera jamais sur une note déjà rencontrée. Pourquoi, au fait ?

Parmi les inconvénients de la gamme de Pythagore, elle ne permet pas de "transposer" ; le problème de la transposition peut se rencontrer dans la situation suivante : on commence à chanter une mélodie jusqu'à ce qu'on réalise qu’on ne va pas pouvoir aller au bout, car les notes à chanter vont devenir trop aiguës pour nous ; nous reprenons donc le chant à partir d'une note de départ plus grave, décalant d'autant les autres notes de manière instinctive avec une justesse plus ou moins heureuse : mais peut-on sur un instrument fabriqué avec une échelle de notes fixées (comme par exemple celui à 8 cordes ci dessus), décaler toutes les notes en conservant l'impression de reconnaître la mélodie ? Ou bien cela impose-t-il des règles pour l’échelle ? 
Les réponses sont "non" à la 1ère question et "oui" à la 2nde.
Autrement dit, si on joue les trois premières cordes, puis les trois dernières, on ne joue pas le " même air ", même décalé.

Voici une mélodie suivie d’une version "transposée" en gardant le même rapport de fréquences d’une note à l’autre que dans la mélodie de départ : si la mélodie est a, b, c alors la transposée est : d, db/a, dc/b

Voici la même mélodie, puis sa version " transposée " en gardant la même différence de fréquences d’une note à l’autre que dans la mélodie de départ : si la mélodie est a, b, c alors la transposée est : d, d + (b – a), d + (c – b)

Si l’on accepte ainsi que, ce qui compte pour reconnaître une mélodie transposée, c’est d’avoir une échelle géométrique (car la seconde écoute, transposition arithmétique, heurte l’oreille en général), on constate que la gamme de Pythagore ne convient pas car les fractions ne sont pas les termes d’une suite géométrique. Voici à nouveau la gamme de Pythagore, une gamme dite " également tempérée ", et enfin les deux superposées

On constate en les entendant simultanément la présence de " battements ", convaincant qu’il y a bien une différence entre les deux... Ainsi, une guitare ou un piano sont conçus théoriquement en respectant une échelle de sons géométrique à 12 notes. Mais il y a d’autres inconvénients car les quintes " justes ", naturelles, ont disparu de l’échelle : c’est-à-dire qu’aucune note n’a plus de fréquence égale aux 2/3 d’une autre note. Un piano, qui serait ainsi construit en théorie, peut donc difficilement s’accorder " justement " avec une personne qui chante. C’est l’avènement des instruments à clavier qui au début du XVIIème siècle a imposé ce choix en Europe. Ces quelques lignes amènent à la conclusion suivante: une gamme est une affaire de compromis, et le nombre de notes est un paramètre influencé à la fois par des raisons culturelles, puisque variable selon les civilisations et les époques, et physiologiques car liés au fonctionnement interne de l'oreille.
On peut trouver au moins une autre raison a posteriori pour expliquer le choix de certaines notes, avec la théorie de Fourier sur les "harmoniques", qui permet sans que cela ait été l'intention initiale de Fourier, une modélisation mathématique des "partiels" d'un son physique.
Mais c'est une autre histoire, qui illustre bien à mon sens l'expression : "la Science permet de mieux comprendre le Monde"...

Sources

[1] SPIESSER Maryvonne.
"Histoire de moyennes. Les moyennes (ou médiétés) arithmétiques, géométriques, harmonique,... dans la Grèce antique."
Publication de l’IREM de Toulouse : http://publimath.irem.univ-mrs.fr/biblio/ITO97002.htm

[2] PROUST Dominique.
" L’harmonie des sphères"
Collection " Science ouverte ", chez Seuil

[3] Bernard PARSZYSZ
" Musique et Mathématiques " 
Brochure de l’APMEP n° 53

 ..................................................................................................................

Image imaginée de Zeriab dans son conservatoire. On remarque sur cette image, des ouds et des tanbours avec ligaments ( frèttes).

                                                            Musicologie :

le mode Sika*, est-il Kurde,  Arabe,  Perse, Turc, Andalous ou Gitan ? Par  Mouats Hafid.

Le mot Sika dans l’ancienne langue persane  est le chiffre trois, c’est le nom de la troisième note de la gamme dite naturelle majeure : Do, ré, MI, fa, sol, la, si  (identifiée par Pythagore, 5 siècle avant J.C  et renommée avec des syllabes d’un hymne par  le moine Guy d’Arezzo, au 11 ^e siècle  après J.C.). C’est aussi  le nom d’un maqam (mode, tabaâ) : Sika (ou segah, sagah)  dans le monde arabo - musulman.

On a rapporté qu’il fut inventé à  l’époque  des premiers  Abbassides par un certain Mohamed Ibrahim El Iraqi. Malgré cette désignation commune aux peuples arabes, turcs et perses, la gamme de ce mode diffère sensiblement d’une région à l’autre. On le trouve mentionné en Andalousie musulmane, parmi les vingt quatre  modes des vingt quatre  noubas.

Ce mode Kurde ( Kourde), a-t-il était ramené par le légendaire Zeriab dans sa fugue de Baghdad vers  Cordoue ?  Ramené avec sa théorie des oudistes, si chère à son maitre Ishaq El Mawsili ?  Celui qui est à l’origine de son émigration  vers l’Occident.  Cet insolent Zeriab,  qui a humilié son maître devant le fameux calife celui des  « mille et une nuits » : Haroun Errachid, était-il d’origine Kurde ? Comme ça était rapporté pour Ibrahim El Mawsili.

Son maitre Ishaq El Mawsili qui l’a affranchi, puisque Zeriab était son esclave et son brillant élève en musique, doit son sobriquet de « Mawssili » (habitant de Mossoul, ville au nord dans le Kurdistan Irakien, et qui existe toujours) à son père Ibrahim qui a fait une escapade d’une année à Mossoul, suite au refus de son père de le laisser pratiquer la musique. Dans le temps où elle fut encore considérée comme distraction réservée aux esclaves et aux marginaux.

 À son retour à Baghdad, Ibrahim qui avait appris la musique chez les Kurdes, station où la musique était pratiquée avec excellence, il fut bien accueilli dans sa famille avec respect et considération, puis,  on l’a prénommé  alors  « Ibrahim El Mawsili ».

De ce fait, des indices notés par des historiens (comme Abou Marwan Ibn Hayyan (mort 1108 après JC) né à Cordoue et El Maqari Shihab al-Din Abul Abbas Ahmad ibn Muhammad ibn Ahmad ben Yahya al Qurayshi, (1591 /1632),   né à  Tlemcen ou bien des musicologues contemporains comme Christian Poché le Franco-Libanais et Mahmoud Guettat le Tunisien) relevaient que Zeriab a certainement eu contact avec Ibrahim El Mawsili à Mossoul. Parmi les  caractéristiques qui penchent sur l’origine kurde  de Zeriab, c’est  son parler,  sa forte éloquence et surtout ses méthodes d’apprentissage du chant, connue sous le nom de : « dudak degmez » (les lèvres ne doivent pas se toucher), une spécificité Kurde et  qu’il avait enseigné à Cordoue. Dans cette région de Mossoul,  il y avait aussi des esclaves noirs qu’on ramenait jusqu’à Baghdad, ainsi, Zeriab le noir avait ce statut, puis il fut libéré (affranchi) comme souligné plus haut  par son maitre Ishaq.

Le nom « Kurde ou kourdi » qui désigne une ethnie ou une région, désigne aussi un « maqam » au moyen - orient ou un « tabaâ »  en Andalousie musulmane, il est l’équivalent de par sa gamme au mode Sika de la musique dite andalouse. On le compare au mode de la Grèce antique : le « Dorien », mais avec un mi bémol à la seconde au lieu d’un mi et un si bémol à sixte au lieu d’un si,:

Le dorien = Ré, mi, fa, sol, la si, do/  un mode qui ne contient donc pas de dièses et bémols 

Sika andalouse = Ré, MI bémol fa, sol, la, SI bémol, do / avec mi bémol  et si bémol.

C’est fort possible que Zeriab utilisait ce mode puisqu’il était connu et enseigné dans l’école des oudistes à Baghdad. On le trouve plus tard après la mort de Zeriab où sa tradition a été longtemps maintenue, sous le nom de « Sika «  parmi les 24 modes et les 24 noubas de l’Andalousie.

 Ce mode - là (Kourde/sika), à partir du 14^e siècle on le découvre  chez les Gitans, troubadours d’Espagne, contemporains des Andalous musulmans qui l’ont pris de la musique arabe et auraient fait leur identité artistique, surtout à Partir du 18^e siècle. Les troubadours descendaient alors  de l’Europe vers l’Andalousie et se sont imprégnés de musique arabe et de leur poésie de la forme métrique du Mouwachah inventé en Andalousie.  Ce mode dépourvu du quart de ton des arabes l’ont adopté au point d’en faire une base de leur musique connue  sous le nom de « flamenco » (mot rapporté à la langue arabe et qui signifie : "felag mengu" (paysan fuyard). Il ya plusieurs versions qui expliquent le sens de ce mot, dont celle de l'historien de la musique Ali Kheder va dans ce sens:

« Pour lui, les Gitans, appelés également Kawali, étaient de fabuleux  "diseurs de bonne aventure" ou (faoualin, en dialecte arabe). Le fait de dire la bonne aventure, de prédire le destin, de dévoiler l'avenir, se dit en arabe  "faala". Par conséquent, le mot "flamenco" serait une légère déformation de "fala min ka" ou "fala min kom", qui veut dire " Il t’a lu (ou il vous a lu) la bonne aventure". » Il appuie sa théorie par l'argument que le flamenco  s'adresse directement aux auditeurs participants, qui interviennent traditionnellement dans la prestation.

On a rapporté aussi que ce mot vient de « flamand » (tailleur de diamants, ou une ethnie de Belgique et de pays bas) que les Arabes ont dénaturé par «  fala mink » puis les Espagnols avaient ajouté le «  O » pour garder ce dernier vocable : Flamenco.

À cette époque là de l’émergence du flamenco, il y a eu  la naissance de la musique à la verticale, c'est-à-dire par  superposition des sons, joués en simultané, qui se diluent  et qui donnent une sensation agréable à l’oreille. C’est la théorie des accords ou l’harmonie, voire polyphonie vocale  et instrumentale. La guitare, instrument dérivé du luth, a été inventé de façon à produire des sons superposés et qui s’y prêtent harmonieusement à cette nouvelle technique, combinée et théorisée autour de deux modes anciens grec, qui sont le mode majeur et mineur ( Lydien et Dorien).

Là, les Gitans avaient transposé le mode Kurde/Sika du ré dorien au mi phrygien pour l’adapter pratiquement au doigté de la guitare. Ainsi la gamme redevienne :

 mi, fa, sol, la, si, do, et ré/  Sika andalouse sur le mi (ou mi bousselik des Arabes)

au lieu de : ré, mi bémol, fa, sol, la, si bémol, do, ré /. Kurde arabe sur le ré ( ré doukah des arabes)

La tierce de cette gamme est mineure (mi / sol)  avec ses 1 ton et ½  demi - ton, que les Gitans par soucis peut - être de variations ou  d’alignement sur l’Occident, l’ont aussi altéré pour rendre sa tierce majeure, (mi / sol dièse) avec ces deux tons, comme ceci :

Mi, fa, sol dièse, la, si, do, ré/ (ce qui donne notre gamme Zidane sur le mi, d’où sa désignation comme sika/zidane dans le jargon du milieu andalous.).  Sika/ zidane, on le trouve dans l’istikhbarats de la nouba mais pas dans ses mélodies. Cette façon de dénaturer le mode sika est surtout appliquée dans la musique populaire : haouzi, aâroubi, chaâbi, rai (comme la très connue chanson : « ya del marsam îdli ma kan ».

*Dans le jargon du milieu de la musique andalouse, de nos jours  dans notre pays, on déforme le mot Sika par « Saika ».

Une dernière précision pour conclure mon analyse, il faut faire une remarque sur le maqam Sika des Arabes et des turcs (les turcs le désignent comme « Segah » ) qui diffère sensiblement de par les intervalles de la gamme :

Sika des arabes du moyen orient : Tonique (qafla) Mi ½ bémol, fa, sol, la, SI ½ bémol, do, ré /

Segah, sagah des turcs et des perses se jouent sur la tonique :

Si ½ bémol altéré, do, ré, Mi ½ bémol altéré, fa dièse, sol, la/

J’écris « altéré » puisque le 1 quart de ton de ces pays n’est pas ½ bémol ou ½ dièse, mais décalé légèrement pas des commas. Déduction : leur mode Sika est le même de par les intervalles (et non le tempérament) que celui des arabes sauf pour les quarts de tons.

J’estime enfin que : Sika, segah et sagah ont la même origine étymologique. Autrefois les pays musulmans s’abreuvaient des mêmes cultures : Byzantine (Syrie), Arabe (Ile arabique), Perse, Turc, Andalouse. Les savants de ces peuples convertis à l’islam utilisaient la langue arabe du coran, pour rédiger des traités et des épitres scientifiques, philosophiques, dogmatiques, etc.  Au point où Al Farabi, Ibn Sina, Tabari, Ibn Roch et d’autres sont considérés par  les mémoires comme arabes.

Mouats Hafid, musicien de Skikda /Algérie, le 27 10 2014.